In recent years, the double-layered multi-head weighers whose hoppers are arranged in two levels are widely used in the accurate and reliable weighing for packing food products. The weighing processes are mathematically modeled into a single objective optimization problems. The objective of packing problem is to minimize the total weight of combined hoppers for a package under the condition that the total weight must be no less than a specified target weight. This paper proposes a novel single objective optimization approach for double-layered multi-head weighing process. More precisely, relying on a new bound on the optimal weight, this study accurately determines the number of hoppers to be combined at each packing operation, and find the best possible hopper combination using the single-objective algorithm. This method significantly speeds up the packing process as a whole. According to the present approach, the candidate number of hoppers to be combined can be taken one or two integral values. The probability that the accurate number of hoppers to be combined becomes one integral value is explicitly calculated, which is the performance factor to the previous one. In addition, results from the numerical experiments to show the effectiveness of the proposed approach are presented.
| Published in | Mathematical Modelling and Applications (Volume 9, Issue 3) |
| DOI | 10.11648/j.mma.20240903.12 |
| Page(s) | 61-69 |
| Creative Commons |
This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited. |
| Copyright |
Copyright © The Author(s), 2024. Published by Science Publishing Group |
Double Layer, Multi-Head Weigher, Packaging Process, Optimization, Single Objective Problem
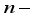 weighing hoppers, a set of
weighing hoppers, a set of 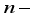 booster hoppers and a discharge chute to the packaging machine (see Figure 1 and Figure 2). Each weighing hopper has its own highly accurate load cell. This load cell will calculate the weight of product in the weighing hopper. The booster hoppers are nothing but the ordinary hoppers without load cell. They are placed underneath of weighing hoppers uprightly or diagonally based on the constructional feature of machine, according to which distinguish the double-layered multi-head weighers upright from diagonal. The packing process begins when the food product is fed into the top of the multi-head weigher, where a dispersal system, normally a vibrating or rotating top cone, distributes the product into a series of linear or radial feeder plates. This top cone is normally equipped with a load cell which controls the feed of product to the multi-head weigher. The linear or radial feeder plates vibrate individually and deliver the food product into the set of
booster hoppers and a discharge chute to the packaging machine (see Figure 1 and Figure 2). Each weighing hopper has its own highly accurate load cell. This load cell will calculate the weight of product in the weighing hopper. The booster hoppers are nothing but the ordinary hoppers without load cell. They are placed underneath of weighing hoppers uprightly or diagonally based on the constructional feature of machine, according to which distinguish the double-layered multi-head weighers upright from diagonal. The packing process begins when the food product is fed into the top of the multi-head weigher, where a dispersal system, normally a vibrating or rotating top cone, distributes the product into a series of linear or radial feeder plates. This top cone is normally equipped with a load cell which controls the feed of product to the multi-head weigher. The linear or radial feeder plates vibrate individually and deliver the food product into the set of 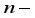 weighing hoppers. The set of weighing hoppers send the food product into the set of
weighing hoppers. The set of weighing hoppers send the food product into the set of 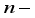 booster hoppers. After each delivery to the weighing and booster hoppers, the linear or radial feeders will stop vibrating and wait until the weighing hoppers have emptied their contents into the booster hoppers before starting again.
booster hoppers. After each delivery to the weighing and booster hoppers, the linear or radial feeders will stop vibrating and wait until the weighing hoppers have emptied their contents into the booster hoppers before starting again. 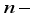 weighing hoppers and
weighing hoppers and 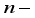 booster hoppers to achieve the desired target weight
booster hoppers to achieve the desired target weight 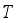 , and chooses some hoppers from the total
, and chooses some hoppers from the total 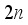 hoppers for a package. Once the calculation is completed, it will open the combined hoppers (hereafter, denote by
hoppers for a package. Once the calculation is completed, it will open the combined hoppers (hereafter, denote by 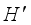 this subset, i.e.
this subset, i.e. 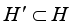 ) and discharge the accurately weighed portion into the packing system or product trays. The resulting empty weighing hoppers (i.e.
) and discharge the accurately weighed portion into the packing system or product trays. The resulting empty weighing hoppers (i.e. 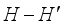 ) are supplied with next new contents of product, and such a packing operation is repeated continuously to produce a large number of food packages one by one.
) are supplied with next new contents of product, and such a packing operation is repeated continuously to produce a large number of food packages one by one. 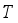 . It is a common knowledge that the number of possible different hopper subsets to be combined is different at each packing operation. This optimization problem that minimize the difference between the combined and the target package weight is known as the NP-complete subset-sum combinatorial one
. It is a common knowledge that the number of possible different hopper subsets to be combined is different at each packing operation. This optimization problem that minimize the difference between the combined and the target package weight is known as the NP-complete subset-sum combinatorial one 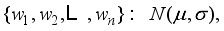
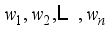 are the real weights of food contents feeded in the weighing hoppers and
are the real weights of food contents feeded in the weighing hoppers and 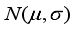 denotes the normal distribution whose mean is
denotes the normal distribution whose mean is 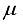 and standard deviation is
and standard deviation is 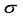 . In the sequel, this paper uses the cumulative distribution function
. In the sequel, this paper uses the cumulative distribution function 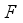 of normal distribution defined by
of normal distribution defined by 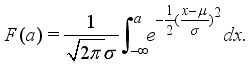
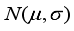 . Since all the weights are independently and identically distributed, the total weight of randomly selected
. Since all the weights are independently and identically distributed, the total weight of randomly selected 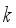 hoppers follows a normal distribution
hoppers follows a normal distribution 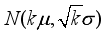 . Thus, One might expect that the average package mean weight
. Thus, One might expect that the average package mean weight 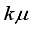 equals to the target weight
equals to the target weight 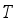 , that is, the number of hoppers
, that is, the number of hoppers 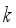 to be combined at each packing operation is constant and fixed in advance, where
to be combined at each packing operation is constant and fixed in advance, where 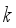 is determined by
is determined by 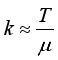 . One might call such
. One might call such 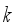 hopper combination are valid hopper combination. Afterawards
hopper combination are valid hopper combination. Afterawards 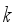 to be combined has previously been defined. However, there is an important problem for choosing
to be combined has previously been defined. However, there is an important problem for choosing 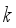 in the industrial setting. Although the weights of food product in the hoppers follow the normal distribution, the average package mean
in the industrial setting. Although the weights of food product in the hoppers follow the normal distribution, the average package mean 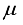 of food product is not the same for all the types of food products. Morever,
of food product is not the same for all the types of food products. Morever, 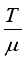 is not always integer in general. For example, if one packs some food product whose target weight
is not always integer in general. For example, if one packs some food product whose target weight 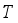 is
is 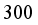 and average package mean
and average package mean 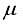 is
is 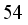 , then the candidate number
, then the candidate number 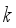 of hoppers to be combined becomes
of hoppers to be combined becomes 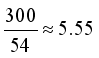 . In such case, it is natural to choose
. In such case, it is natural to choose 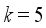 and
and 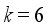 . In other words, one must find the optimal weight among both
. In other words, one must find the optimal weight among both 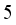 and
and 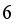 hopper combinations. It will reduce the computational time if it is proved that only
hopper combinations. It will reduce the computational time if it is proved that only 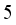 hopper or only
hopper or only 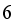 hopper combinations are valid. The computational cost of generating and evaluating all the valid hopper combinations is closely related to the accurate determination of the number of hoppers to be combined from the candidate numbers. This problem becomes more difficult when the entire number of hoppers are large, especilly when the double-layered multihead weighing process work.
hopper combinations are valid. The computational cost of generating and evaluating all the valid hopper combinations is closely related to the accurate determination of the number of hoppers to be combined from the candidate numbers. This problem becomes more difficult when the entire number of hoppers are large, especilly when the double-layered multihead weighing process work. 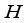 : Set of total
: Set of total 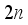 hoppers.
hoppers. 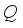 : The total number of packages needed.
: The total number of packages needed. 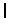 : Current iteration number of packing operation.
: Current iteration number of packing operation. 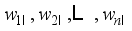 : The weights of food product in the weighing hoppers at
: The weights of food product in the weighing hoppers at 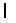 -th packing operation.
-th packing operation. 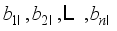 : The weights of food product in the booster hoppers at
: The weights of food product in the booster hoppers at 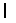 -th packing operation.
-th packing operation. 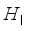 : Set of all hopper combinations at
: Set of all hopper combinations at 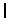 -th packing operation.
-th packing operation. 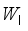 : The total weight calculated as the sum of the weight in
: The total weight calculated as the sum of the weight in 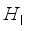 hoppers at
hoppers at 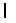 -th packing operation.
-th packing operation. 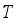 : Target weight.
: Target weight. 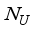 of combinations for the upright type double-layered weighing process when the fixed
of combinations for the upright type double-layered weighing process when the fixed 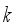 hoppers are combined is calculated by
hoppers are combined is calculated by 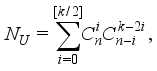 (1)
(1) 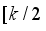 ] denotes the integer part of
] denotes the integer part of 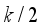 . It was also proved in
. It was also proved in 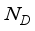 of combinations for the diagonal type double-layered weighing process when the fixed
of combinations for the diagonal type double-layered weighing process when the fixed 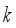 hoppers are combined is computed by
hoppers are combined is computed by 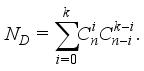 (2)
(2) 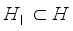 at every packing operation such that some weight
at every packing operation such that some weight 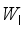 is minimized under the condition that
is minimized under the condition that 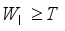 . The
. The 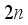 -dimensional binary vectors
-dimensional binary vectors 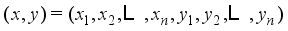 is defined as follows.
is defined as follows. 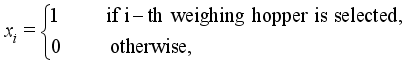
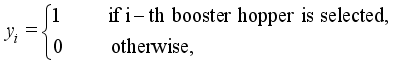
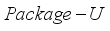 is formulated as follows.
is formulated as follows. 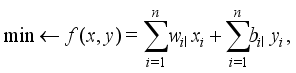 (3)
(3) 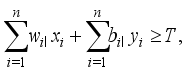 (4)
(4) 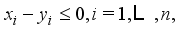 (5)
(5) 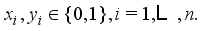 (6)
(6) 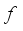 of (3) aims at attaining the total weight of selected hoppers as close to the target weight
of (3) aims at attaining the total weight of selected hoppers as close to the target weight 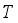 as possible, under the condition (4) (i.e., the target weight constraint). The equation (5) reflects the constructional feature of upright type that it cannot choose the
as possible, under the condition (4) (i.e., the target weight constraint). The equation (5) reflects the constructional feature of upright type that it cannot choose the 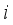 -th weighing hopper unless it chooses the
-th weighing hopper unless it chooses the 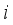 -th booster hopper. A solution
-th booster hopper. A solution 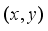 satisfying (4)-(6) is referred to as a feasible solution of the problem
satisfying (4)-(6) is referred to as a feasible solution of the problem 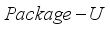 . Moreover, for the problem
. Moreover, for the problem 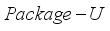 ,
, 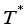 is denoted by the minimum of the total weight of a feasible solution
is denoted by the minimum of the total weight of a feasible solution 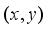 . An optimal solution
. An optimal solution 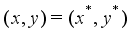 is defined as a feasible solution satisfying
is defined as a feasible solution satisfying 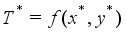 .
.  is formulated as follows.
is formulated as follows. 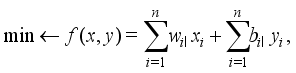 (7)
(7) 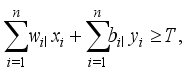 (8)
(8) 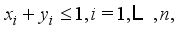 (9)
(9) 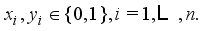 (10)
(10) 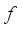 of (7) aims at attaining the total weight of selected hoppers as close to the target weight
of (7) aims at attaining the total weight of selected hoppers as close to the target weight 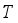 as possible, under the condition (8) (i.e., the target weight constraint). The equation (9) reflects the constructional feature of diagonal type that it cannot choose the
as possible, under the condition (8) (i.e., the target weight constraint). The equation (9) reflects the constructional feature of diagonal type that it cannot choose the 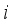 -th weighing hopper unless it chooses the
-th weighing hopper unless it chooses the 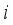 -th booster hopper. A solution
-th booster hopper. A solution 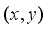 satisfying (8)-(10) is referred to as a feasible solution of the problem
satisfying (8)-(10) is referred to as a feasible solution of the problem 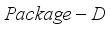 . Moreover, for the problem
. Moreover, for the problem 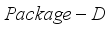 ,
, 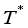 is denoted the minimum of the total weight of a feasible solution
is denoted the minimum of the total weight of a feasible solution 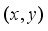 . An optimal solution
. An optimal solution 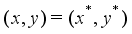 is defined as a feasible solution satisfying
is defined as a feasible solution satisfying 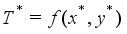 .
. 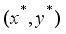 be the optimal solution that satisfies
be the optimal solution that satisfies 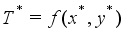 for both problems
for both problems  and
and 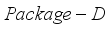 . Then it holds that
. Then it holds that 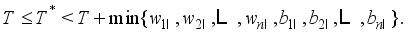 (11)
(11) 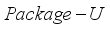 is proved. Since the optimal solution
is proved. Since the optimal solution 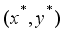 is a feasible one with the target weight constraint (4), the left hand side inequality of (11) holds. By the optimality of
is a feasible one with the target weight constraint (4), the left hand side inequality of (11) holds. By the optimality of 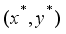 , it holds that
, it holds that 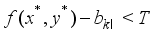 (12)
(12) 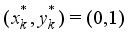 . If the converse inequality
. If the converse inequality 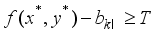 holds, then it implies that deleting
holds, then it implies that deleting 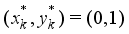 from the optimal solution becomes another feasible solution, and it contradicts the optimality of
from the optimal solution becomes another feasible solution, and it contradicts the optimality of 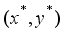 . Similarly, it also holds that
. Similarly, it also holds that 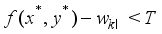 (13)
(13) 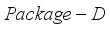 is proved. Since the optimal solution
is proved. Since the optimal solution 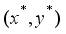 is a feasible one with the target weight constraint (8), the left hand side inequality of (11) also holds for the problem
is a feasible one with the target weight constraint (8), the left hand side inequality of (11) also holds for the problem  . By the optimality of
. By the optimality of 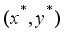 , it holds that
, it holds that 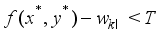 (14)
(14) 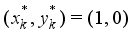 . If the converse inequality
. If the converse inequality 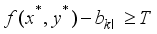 holds, then it implies that deleting
holds, then it implies that deleting 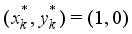 from the optimal solution becomes another feasible solution for the problem
from the optimal solution becomes another feasible solution for the problem 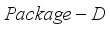 , and it contradicts the optimality of
, and it contradicts the optimality of 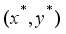 . In the similar fashion as above, it also holds that
. In the similar fashion as above, it also holds that 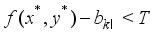 (15)
(15) 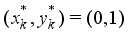 . Therefore, the right hand side inequality of (11) holds for the problem
. Therefore, the right hand side inequality of (11) holds for the problem 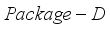 . Finally, the theorem is proved.
. Finally, the theorem is proved. 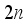 hoppers follow independently and identically a normal distribution
hoppers follow independently and identically a normal distribution 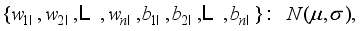 (16)
(16) 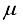 is the average package weight and
is the average package weight and 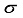 is the standard deviation. Garcia-Diaz et al.
is the standard deviation. Garcia-Diaz et al. 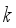 to be combined at each packing operation is constant and fixed in advance, where
to be combined at each packing operation is constant and fixed in advance, where 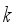 is determined by
is determined by 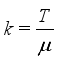 and the set of all possible
and the set of all possible 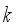 -hopper combinations becomes valid hopper combinations. As already mentiond in section 1,
-hopper combinations becomes valid hopper combinations. As already mentiond in section 1, 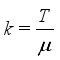 is not always integer for any
is not always integer for any 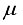 and
and 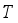 . It is hard to fix
. It is hard to fix 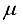 such that
such that 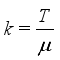 becomes an integer in the real industrial settings.
becomes an integer in the real industrial settings. 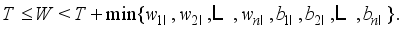
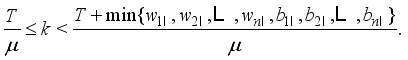 (17)
(17) 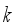 is defined in detail.
is defined in detail. 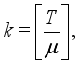 if
if 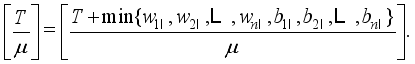 (18)
(18) 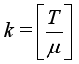 and
and 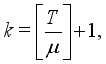 if
if 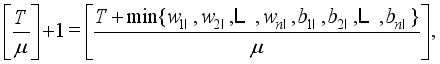 (19)
(19) 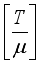 denotes the integer part of
denotes the integer part of 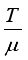 .
. 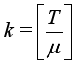 is explicitly calculated. This probability is computed by (18) and using the property of extreme distribution
is explicitly calculated. This probability is computed by (18) and using the property of extreme distribution 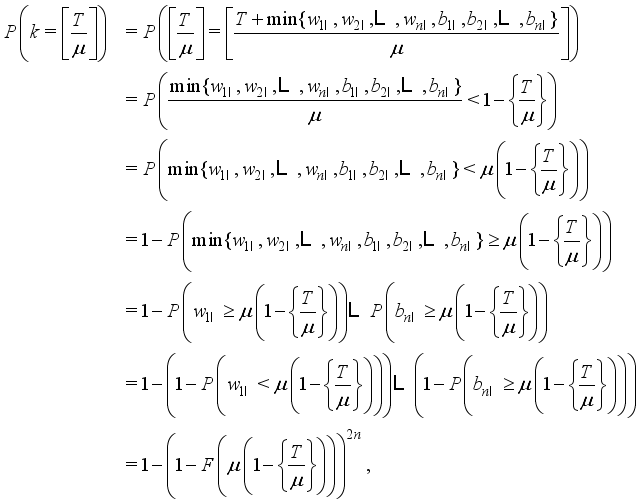 (20)
(20) 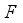 is the cumulative distribution function of normal distribution. From (20), one concludes that this probability increases when the total number of hoppers
is the cumulative distribution function of normal distribution. From (20), one concludes that this probability increases when the total number of hoppers 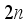 increases.
increases. 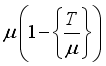 .
. 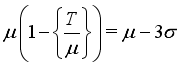 , then one has from Figure 3 that
, then one has from Figure 3 that 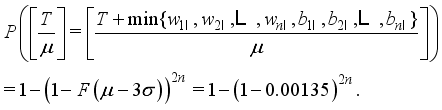 (21)
(21) 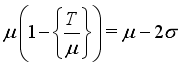 , then one has from Figure 3 that
, then one has from Figure 3 that 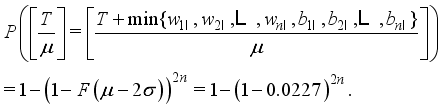 (22)
(22) 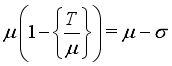 , then one has from Figure 3 that
, then one has from Figure 3 that 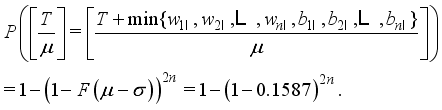 (23)
(23) 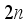 -Total number of hoppers,
-Total number of hoppers,  -Number of hoppers involved in each packing operation (
-Number of hoppers involved in each packing operation ( 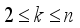 ),
), 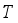 -Target weight (
-Target weight ( 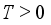 ),
), 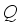 -Total number of packages to be produced,
-Total number of packages to be produced, 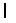 -Iteration number of packing (
-Iteration number of packing ( 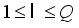 ),
), 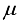 -Average package weight of food product,
-Average package weight of food product, 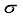 -Standard deviation of the weights supplied to each hopper.
-Standard deviation of the weights supplied to each hopper. 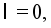 and
and 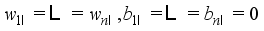 for all
for all 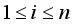 .
. 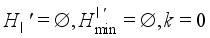 .
. 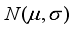 is assigned.
is assigned. 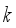 of hoppers to be combined as follows.
of hoppers to be combined as follows. 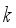 hopper combinations. If sum weight is less than the target weight
hopper combinations. If sum weight is less than the target weight 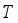 , then delete this combination from
, then delete this combination from 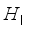
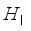 .
. 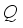 packets has been completed, the process ends. Otherwise, it returns to Step 3.
packets has been completed, the process ends. Otherwise, it returns to Step 3. 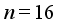 , the total weight
, the total weight 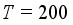 , the average package mean
, the average package mean 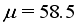 and the total number of packages to be produced
and the total number of packages to be produced 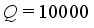 . Then the candidate number of valid hopper
. Then the candidate number of valid hopper 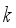 is calculated by
is calculated by 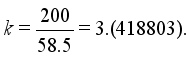
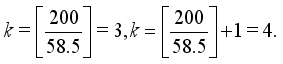
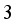 -hopper combinations and
-hopper combinations and 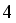 -hopper combinations at every packing, i.e. the total number of combinations is computed by (1) and (2), respectively.
-hopper combinations at every packing, i.e. the total number of combinations is computed by (1) and (2), respectively. 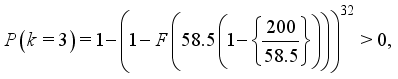 (24)
(24) min | Minimize |
| [1] | Barreiro, J. J., González, C., Salicrú, M., Optimization of multiweighing packing proceeding, Top, 1998, 6 (1), 37-44. |
| [2] | Beretta, A. and Semeraro, Q. On a RSM approach to the multihead weigher configuration, in the 11th biennial Conference on Engineering Systems Design and Analysis (ASME 2012), Nantes, France, 225-233. |
| [3] | Beretta, A., Sraro, Q., Del Castillo, E., On the Multihead Weigher Machine Setup Problem, Packag. Technol. Sci., 2016, 29, 175-188. |
| [4] | Dekking, F. M., Kraaikamp, C., Lopuhaä, H. P., Meester, L. E., A Modern Introduction to Probability and Statistics, Springer, Berlin, 2005. |
| [5] | Del Castillo, E., Beretta, A., Semeraro, Q., Optimal setup of a multihead weighing machine, Eur. J. Oper. Res., 2017, 259, 384-393. |
| [6] | Erdogdu, F., Optimization in Food Engineering, Taylor & Francis, London, 2009. |
| [7] | Garcia-Diaz, J. C., Pulido-Rojano, A., Giner-Bosch, V., Bi-objective optimisation of a multihead weighing process, Eur. J. Ind. Eng., 2017, 11, 403-423. |
| [8] | Garica-Diaz, J. C., Pulido-Rojano, A., Monitoring and control of the multihead weighing process through a modified control chart, DYNA, 2017, 84, 135-142. |
| [9] | Garcia-Jiménez, R., Garica-Diaz, J. C., Pulido-Rojano, A. D., Packaging Process Optimization in Multihead Weighers with Double-Layered Upright and Diagonal Systems, Mathematics, 2021, 9, 1039, 1-20. |
| [10] | Garcia-Jiménez, R., Garica-Diaz, J. C., Pulido-Rojano, A. D., Bicriteria food packaging process optimization in double-layered upright and diagonal multihead weighers, J. Comput. Appl. Math., 2023, 428, 115168. |
| [11] | Garey, M. R. and Johnson, D. S., Computers and Intractability: A guide to the theory of NP-completeness, WH Freeman & Company, 1979. |
| [12] | Imahori, S., Karuno, Y., Nagamochi, H., Wang, X., Kansei engineering, humans and computers: Efficient dynamic programming algorithms for combinatorial food packing problems, Int. J. Biomet., 2011, 3, 228-245. |
| [13] |
Imahori, S., Karuno, Y., Tateishi, K., Dynamic programming algorithms for producing food mixture packages
by automatic combination weighers, Journal of Advanced Mechanical Design, Systems, and Manufacturing, Vol. 8, No. 5, (2014), https://doi.org/10.1299/jamdsm.2014jamdsm0065 |
| [14] | Ishida Co., Ltd., Products (Total System Solutions), Weighing and Packaging, 2015, Available from: |
| [15] | Karuno, Y., Nagamochi, H., Wang, X., Bi-criteria food packing by dynamic programming, J. Oper. Res. Soc. Jpn., 2007, 50, 376-389. |
| [16] | Karuno, Y., Nagamochi, H., Wang, X., Optimization Problems and Algorithms in Double-layered Food Packing Systems, J. Adv. Mech. Des. Syst. Manuf., 2010, 4, 605-615. |
| [17] | Karuno, Y., Takahashi, K., Yamada, A., Dynamic Programming Algorithms with Data Rounding for Combinatorial Food Packing Problems, J. Adv. Mech. Des. Syst. Manuf., 2013, 7, 233-243. |
| [18] | Keraita, J. N., Kim, K. H., A study on the optimum scheme for determination of operation time of line feeders in automatic combination weighers, J. Mech. Sci. Technol., 2006, 20, 1567-1575. |
| [19] | Keraita, J. N., Kim, K. H., A Weighing Algorithm for Multihead Weighers, Int. J. Precis. Eng. Manuf., 2007, 8, 21-26. |
| [20] | Montgomery, D. C., Introduction to Statistical Quality Control, 6th ed., John Wiley & Sons, 2009. |
| [21] | Nurcahyadi, T., Blum, C., Ant colony optimization for packing process optimization in multi-head weigher machines, Aip conf. Proc., 2023, 2837, 02001. |
| [22] | Pulido-Rojano, A., Garcia-Diaz, J. C., Giner-Bosch, V., A multiobjective approach for optimization of the multihead weighing process, Proceedings of the International Conference on Industrial Engineering and Systems Management, Seville, Spain, 2015, 426-434. |
| [23] | Pulido-Rojano, A. and Garcia-Daz, J. C.. Analysis of the filling setting in the multihead weighing process, in Proceedings of the International Joint Conference, CIO-ICIEOM-IIE-AIM (IJC 2016), San Sebastián, Spain, 2016, 521-528. |
| [24] | Pulido-Rojano, A., Garcia-Daz, J. C., Optimisation algorithms for improvement of a multihead weighing process, Int. J. Prod. Qual. Manag., 2020, 29, 109-125. |
APA Style
An, P., Hong, C., Ri, R., Yu, C., O, C. (2024). An Improved Single Objective Optimization Approach for Double-Layered Multi-Head Weighing Process. Mathematical Modelling and Applications, 9(3), 61-69. https://doi.org/10.11648/j.mma.20240903.12
ACS Style
An, P.; Hong, C.; Ri, R.; Yu, C.; O, C. An Improved Single Objective Optimization Approach for Double-Layered Multi-Head Weighing Process. Math. Model. Appl. 2024, 9(3), 61-69. doi: 10.11648/j.mma.20240903.12
AMA Style
An P, Hong C, Ri R, Yu C, O C. An Improved Single Objective Optimization Approach for Double-Layered Multi-Head Weighing Process. Math Model Appl. 2024;9(3):61-69. doi: 10.11648/j.mma.20240903.12
@article{10.11648/j.mma.20240903.12,
author = {Pom An and Chol-Jun Hong and Ryong-Yon Ri and Chol-Jun Yu and Chol-Jun O},
title = {An Improved Single Objective Optimization Approach for Double-Layered Multi-Head Weighing Process
},
journal = {Mathematical Modelling and Applications},
volume = {9},
number = {3},
pages = {61-69},
doi = {10.11648/j.mma.20240903.12},
url = {https://doi.org/10.11648/j.mma.20240903.12},
eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.mma.20240903.12},
abstract = {In recent years, the double-layered multi-head weighers whose hoppers are arranged in two levels are widely used in the accurate and reliable weighing for packing food products. The weighing processes are mathematically modeled into a single objective optimization problems. The objective of packing problem is to minimize the total weight of combined hoppers for a package under the condition that the total weight must be no less than a specified target weight. This paper proposes a novel single objective optimization approach for double-layered multi-head weighing process. More precisely, relying on a new bound on the optimal weight, this study accurately determines the number of hoppers to be combined at each packing operation, and find the best possible hopper combination using the single-objective algorithm. This method significantly speeds up the packing process as a whole. According to the present approach, the candidate number of hoppers to be combined can be taken one or two integral values. The probability that the accurate number of hoppers to be combined becomes one integral value is explicitly calculated, which is the performance factor to the previous one. In addition, results from the numerical experiments to show the effectiveness of the proposed approach are presented.
},
year = {2024}
}
TY - JOUR T1 - An Improved Single Objective Optimization Approach for Double-Layered Multi-Head Weighing Process AU - Pom An AU - Chol-Jun Hong AU - Ryong-Yon Ri AU - Chol-Jun Yu AU - Chol-Jun O Y1 - 2024/09/06 PY - 2024 N1 - https://doi.org/10.11648/j.mma.20240903.12 DO - 10.11648/j.mma.20240903.12 T2 - Mathematical Modelling and Applications JF - Mathematical Modelling and Applications JO - Mathematical Modelling and Applications SP - 61 EP - 69 PB - Science Publishing Group SN - 2575-1794 UR - https://doi.org/10.11648/j.mma.20240903.12 AB - In recent years, the double-layered multi-head weighers whose hoppers are arranged in two levels are widely used in the accurate and reliable weighing for packing food products. The weighing processes are mathematically modeled into a single objective optimization problems. The objective of packing problem is to minimize the total weight of combined hoppers for a package under the condition that the total weight must be no less than a specified target weight. This paper proposes a novel single objective optimization approach for double-layered multi-head weighing process. More precisely, relying on a new bound on the optimal weight, this study accurately determines the number of hoppers to be combined at each packing operation, and find the best possible hopper combination using the single-objective algorithm. This method significantly speeds up the packing process as a whole. According to the present approach, the candidate number of hoppers to be combined can be taken one or two integral values. The probability that the accurate number of hoppers to be combined becomes one integral value is explicitly calculated, which is the performance factor to the previous one. In addition, results from the numerical experiments to show the effectiveness of the proposed approach are presented. VL - 9 IS - 3 ER -